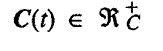
A
Quiet Revolution in Welfare Economics- by Michael Albert and Robin Hahnel
Our new evaluative theory is based on our new paradigm and specifically our theory of natural, species, and derived needs. Our most general statement of how to evaluate the performance of any set of economic institutions is to ask whether or not those institutions serve to maximize human fulfillment and development. We must obviously clarify what we mean by this and how we propose to "measure" welfare conceived in this way. But it is worth pointing out before beginning, that our approach obviously goes beyond the traditional notion of efficiency in satisfying peoples' manifest preferences by insisting on also evaluating the development of needs themselves. In the previous chapter we explained how people have a variety of natural and species needs such as needs for food, shelter, sexual gratification, knowledge, affection, self-esteem, social recognition, and selfmanagement. It is obviously a good thing to fulfill these needs to the greatest extent possible. But these needs never exist in a "pure form." They are always expressed through a host of derived needs like those for particular types of food, marriage to a particular person, a car of a certain make and model, etc. Under no circumstances do we call any of these derived needs "false needs," since once they exist they are no less urgent than our underlying natural and species needs, which are expressed through particular derived needs in any case. But, like John Stuart Mill before us, we cannot convince ourselves that maximum fulfillment of different sets of derived needs necessarily yields the same degree of satisfaction. As we explained in the previous chapter, it is perfectly possible to develop detrimental character traits that can take on a structural life of their own by defining derived needs whose fulfillment generates less well-being than would be experienced by the fulfillment of a different set of derived needs. Therefore, the development of derived needs is just as much the proper subject matter of evaluative theory as is the fulfillment of derived needs. In short, we will not take the "ostrich" approach to the admittedly difficult problem of need development.
In the first section we use concepts from the previous chapter to develop a
formal model of a person with endogenous preferences. In the second section
we use the model to derive a series of theorems that establish interesting welfare
theoretic results. In some cases the results contradict traditional conclusions,
and in other cases the results contradict the intuitions of other pioneers in
the theory of endogenous preferences. As we will see, endogenous preferences
raise issues traditional theory is blind to, pose fewer difficulties for fundamental
welfare theorems than some pioneers believed, yet imply a far more disturbing
interpretation of nonoptimalities and their consequences than hitherto recognized.
But while all this is demonstrated with a model that does not entail any explicit
evaluation of different developmental trajectories, much in our welfare theory
proceeds from an explicit evaluation of alternative human development patterns.
We take up these critical matters in the final section of the chapter, only
after demonstration of what should be noncontroversial results-a strategy in
the best tradition of welfare economics.
We seek a formalism expressing the fact that activities not only fulfill existing needs or preferences but change or develop those preferences as well. The first step is to stipulate that while the fulfillment individuals derive from participating in a particular set of activities obviously depends on their preferences, those preferences in turn depend on the human characteristics individuals possess at the time. In other words, individuals' "instantaneous" preference orderings are parameterized by their "instantaneous" human characteristics. In this way individuals' "needs" change whenever any of their human characteristics change-which is what we mean by "derived needs."
M 1.1. Let U(t) represent an individual's instantaneous preference ordering at time t , and
M 1.2. Let C(t) represent the whole array of personality traits, skills, knowledge, and values a person has in period t. In other words C(t) = [ P(t), S(t), K(t), V(t) ] where each vector inside the brackets has many components as well, as discussed in chapter 5. For convenience we will assume C(t) is a vector with C components where each component is a postive real number, so that
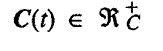
M 1.3. The fulfillment, satisfaction, or utility achieved in period
t becomes U(t)
= U(P(t), S(t), K(t), V(t);
(.)) or, U(t) = U(C(t); (.)) where
(.) represents all the economic activities in period t that in any way
affect the individual's wellbeing.
In general, an individual's instantaneous preference ordering should be defined on "activity space." That is, one's satisfaction is a function of all the activities carried out by groups in which one, in some sense, participates. In terms of the notation of chapter 5, (.) would be all the activities Ak(i,t) carried out by groups i in which the individual participates.1
But for present purposes, we can adopt the traditional view that all welfare
significant activities in which people participate can be interpreted as the
consumption and laboring activities each carries out individually, which in
turn are assumed to be fully described by the quantities of different "consumption
goods" each consumes, and the number of hours each works in different kinds
of job categories. While the more general conceptualization of individuals participating
in various elements of group activity space is more appropriate to treatment
of issues such as public goods and the labor process, for many issues that have
been the primary focus of welfare theory, the traditional formulation is sufficient,
and these are the issues we address first. So for now,
![]()
be a vector whose elements represent quantities of each commodity consumed by
the individual at time t
so that
![]()
![]() be a vector whose elements represent
hours of different kinds of labor the individual carries out at time t,
be a vector whose elements represent
hours of different kinds of labor the individual carries out at time t,
![]() 2
2
And instead of describing the welfare significant activity space for an individual
at time t as (.)
= Ak(i,t) where k
ranges over all activities, and i
ranges over all the groups the individual "participates in"--broadly definedwe
describe it as the commodities consumed and labor done by the individual in
period t or:
![]()
![]() And for convenience we define U(t)
as a continuous, differentiable function mapping elements from
And for convenience we define U(t)
as a continuous, differentiable function mapping elements from
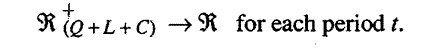
The second step, which makes preferences "endogenous," is to stipulate that
these various human characteristics are potentially functions of economic activities
previously carried out. In this way participating in any economic activity has
both what we call a "preference fulfillment effect"-- fulfills present preferences
to a greater or lesser extent-and what we call a "preference development effect"--it
influences future character structures, which in turn influence future preference
orderings.
M 1.8. For each element i of an individual's personality
characteristic vector P(t):
pi(t)
= pi(Q(t-1), Q(t-2),..
. Q(0); L(t-1), L(t-2).... L(0))
And, similarly, for the other individual human state variables:
si(t)
= si( Q(t-l), Q(t-2),. .. Q(0); L(t-1),
L(t-2) .... L(0))
ki(t) = ki( Q(t-1), Q(t-2)....
Q(0); L(t-1), L(t-2) .... L(0))
vi(t) = vi(Q(t-1), Q(t-2),. .. Q(0);
L(t-1), L(t-2) .... L(0))
And for convenience we define each characteristic formation function at each
point in time, as a continuous, differentiable function mapping elements from
Â+t(Q+L)to Â+.
M 1.9. Finally, the well-being an individual enjoys over his or her life would simply be some function of the well-being achieved in all time periods so that:
W =
W(U(0),... U(T)).
M 1.10. But for our purposes nothing is lost by specifying an overall wellbeing function that is a linear function of fulfillment in each time period where tt represents the individual's subjective rate of time discount for fulfillment in period t. So W is a linear function mapping elements in Â(T+1) to  .
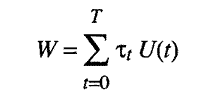
We complete our model of an individual with endogenous preferences with the
budget constraint. We abstract from two complications irrelevant to our present
purposes: income from initial stocks other than laboring capacities and borrowing
and lending. For now there is no harm in specifying that expenditures in each
period must be paid out of earnings in the same period.
3
M 1. 11. Let I(t)
be income in period t,
a continuous, differentiable function mapping elements in Â+(C+L)
to Â+,
where
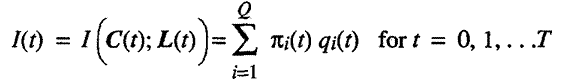
where pi(t) is the price the individual must pay for a unit of good i in period t, and the nonsatiation axiom justifies the equality. Or, using vector multiplication
I(t) = p(t)•Q(t) is our budget constraint in each time period.
Although we agree with Gintis that a host of uncertainties is involved in any
individual's estimation of these parameterized utility functions and human characteristic
development functions, we choose to ignore these "uncertainty" issues. This
is not because we think they are uninteresting, but because we have "other fish
to fry." The theorems of this and subsequent chapters are our justification
for the strategic decision to abstract from uncertainty by extending the assumption
of "perfect knowledge" of traditional welfare theory to the new context of endogenous
preferences. We will grant people "perfect knowledge" not only of the degree
to which different "consumption-work bundles" fulfill their preferences of the
moment and the relative prices and wages of different goods and jobs today,
but "perfect knowledge" of how different consumption-work bundles chosen today
will modify their future characteristics and how these new characteristics will
change their preferences. Once again, the mere statement of the assumptions
reinforces the reasonableness of Gintis' practical objections. But Debreu had
already extended the perfect knowledge assumption to future prices and preference
fulfillment effects in the spirit of the traditional welfare project-uncovering
the implications of informed, individual, rational choice. In the same spirit
we waive Gintis' objection.
Traditional welfare theory teaches us how to estimate the welfare
effects of economic choices. It interprets coincidence of relative supplies
and desires as worthy of praise. And it establishes three "fundamental" theorems
concerning the welfare characteristics of competitive, private enterprise market
economies. Under appropriate assumptions:
1. At least one general equilibrium exists for any competitive,
private enterprise market economy
2. Any general equilibrium of a competitive, private enterprise
market economy is Pareto optimal
3. Any Pareto optimal outcome can be achieved as the general equilibrium
of a perfectly competitive, private enterprise economy with the appropriate
initial endowments
But traditional theorems assume exogenous preferences, so our first task is
to reexamine traditional lessons under the assumption of endogenous rather than
exogenous preferences as we model the phenomenon. In addition to being a matter
of standard procedure in the development of what Kuhn termed "normal science,"
reexamination is necessary because Gintis claimed traditional welfare theory
systematically misestimates and misinterprets welfare effects and that the second
fundamental theorem of welfare economics is false under the assumption of endogenous
preferences. Pollak, El Safty, and Hammond claim no fundamental conclusions
are altered by treating preferences as endogenous unless welfare conclusions
become impossible to draw altogether. Clarification is in order before we present
our own view of how endogenous preferences are related to the fundamental issues
of welfare economics. 4
Treating preferences as endogenous certainly changes estimation of the welfare effects of specific actions and undermines the traditional interpretation of the welfare significance of coincidence between supplies and demands in partial equilibrium settings.
Misestimating Welfare Effects. Gintis was perfectly correct in
pointing out that traditional theory misestimates the welfare effects of economic
choices if consumption-work choices not only fulfill present preferences more
or less satisfactorily, but also change future preferences by changing future
human characteristics, thereby affecting the possibilities of obtaining satisfaction
from future consumption-work possibilities. We formulate and demonstrate this
proposition as Theorem 6.1.
|
THEOREM 6.1: MISESTIMATING WELFARE EFFECTS. A neoclassical welfare theory that ignores the fact that present choices of consumption and work activities not only fulfill present preferences but also generate changes in future preferences will systematically misestimate the welfare effects of economic choices. 5 |
The theorem is intuitively plausible since any theory that fails to consider
a significant relationship would be expected to misestimate effects of related
actions. However, to prove the proposition requires some effort and the results
are illustrative.
First, if we adopt the conventional assumption that all functions are continuous
and differentiable, and the convenient assumptions of an interior solution point
and binding budget constraints, we can model the individual's welfare maximization
choice as a "classical programming problem. " 6
We write the Lagrangian
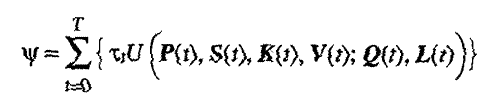
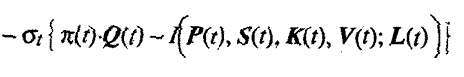
Remembering that the choice variables are simply the quantities of each good to consume in each period and the number of hours to work at each different kind of labor activity in each period, we write the first order necessary conditions for a welfare maximum
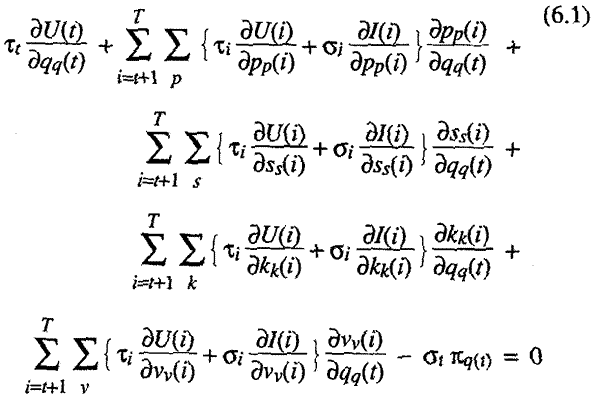
For t =
0 ... t and q = 1 ...
Q there would be (T+1)
times Q equations of
the above type. And
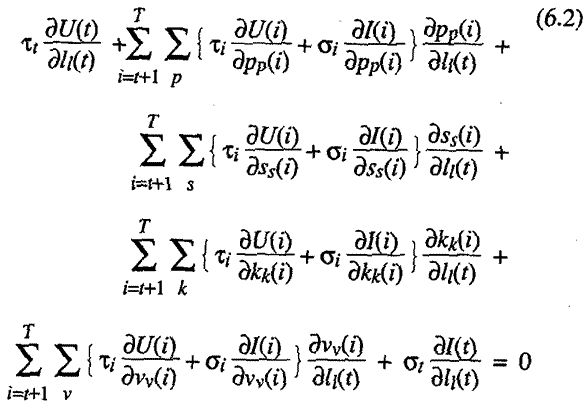
For t
= 0 ... T
and l
= 1 ... L there would (T+1)
times L equations of
the above type. And finally
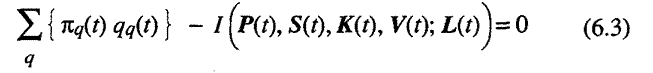
where for t = 0
... t there
would be (T+1)
"budget constraint" equations of the above sort. The result we are seeking follows
directly from observing that if preferences are endogenous we cannot assume
that the first set of terms under the double summation in both (6.1) and (6.2)
are zero. Quite the contrary, in the presence of "preference development effects"
there is every reason to believe their sum can be either positive or negative.
Von Weizsacker, Hammond, and especially Pollak were not primarily concerned
with the welfare effects of endogenous preferences - particularly conceived
as fully informed rational self-molding. But it is difficult to imagine they
would disagree with this conclusion. That few, if any, traditional theorists
would disagree is even more apparent once one recognizes the similarity between
this result and analogous results in human capital theory that have been long
acknowledged.
Prior to the advent of human capital theory all the terms under the double summation
signs were ignored in expressions (6.1) and (6.2). Human capital theory recognized
the need for including the effects of the second set of terms under the summation
signs. In (6.1) those effects are interpreted as "consumption" choices that
are, at least in part, "investments" in "human capital." In (6.2) those effects
are conceived as "on-the-job training" effects of work activities.
Human capital theory pointed out that a welfare theory that ignored the human
capital and on-the-job training effects of consumption and work activity choices
misestimates welfare effects by ignoring the effects on individuals' future
budget constraints. A theory of endogenous preferences makes a completely analogous
point; a welfare theory that ignores the effects of consumption and work activity
on individuals' future preferences necessarily misestimates welfare effects
by ignoring the effects on individuals' capacity to extract satisfaction from
future options.
Presumably the only difference between Gintis, on the one hand, and von Weizsacker,
Hammond, and Pollack, on the other, would be how much importance they attach
to this new revelation-and whether to consider it reason to look for a new welfare
paradigm. In any case, Gintis would no doubt agree that the necessary "correction"
can easily be made as it was in the case of human capital theory, and as he,
himself, has done.
Misinterpreting Coincidence of Supplies with Demands. Gintis' observation is correct. If people mold their desires to better coincide with the terms of availability that exist independently of those desires, the positive welfare implications of a coincidence between relative supplies and desires vanish. We demonstrate this claim as Theorem 6.2.
In traditional theory it was possible to "separate" supply and
demand. As long as we treated preferences as exogenous, there was no possibility
that demands could adjust to supplies. In this case, equality between ratios
of marginal costs of supplying activities and ratios of marginal utilities for
those activities was of great welfare significance because it occurred only
if the "economy" supplied activities according to people's relative desires.
7 But Theorem 6.2 challenges
the welfare significance traditionally imputed to "consumer sovereignty" as
judged by people's "instantaneous preference orderings." Once demand is a function
of supply, traditional partial equilibrium welfare theory goes by the wayside.
For convenience, our demonstration of Theorem 6.2 concerns a change
in the relative prices of two goods in the last period, T.
Then we explain why the result can be generalized to a change in relative prices
in any period.
Suppose there is a change in the relative prices of the mth and nth
commodities in period T,
pm(T)
and pn(T)A.
superscript A signifies prices after the change and a superscript O
signifies original prices. We change the relative terms of supply by increasing
the price of m relative
to n in period T.
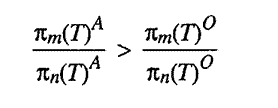
Since we are in the last time period, no terms are inside the double summation
sign for T and commodity
m and for T
and commodity n in
expression (6.1) under either the new or the old price system. So if the individual
maximizes his or her welfare in each situation we are led directly to the conclusion:

The assumption of diminishing marginal utilities
8 yields
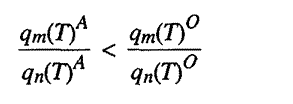
But a change in the relative proportions of commodities m and n consumed
in period T will change
the values of partial derivatives of utility in period T
with respect to all the human characteristics found under the summation signs
in all the necessary conditions for all the previous time periods since these
partials are still functions of the quantities of commodities m
and n in period T.
Letting a(t)
stand for any of our human characteristics, we can conclude that if ai(t)
increases enjoyment of commodity m
relative to commodity n,
then:
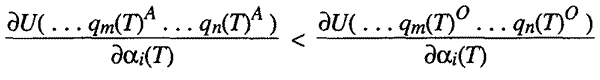
Alternatively, if ai(t)
increases enjoyment of n
relative to m,
then:
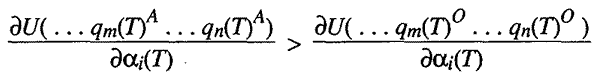
Although it is possible, there is no reason to suppose that the sum total effects
of changes in the values of these partials in any one of the necessary conditions
for q
= 1 ... Q and t
= 0 ... (T-1)
would be such as to exactly cancel out at the old values of consumption and
work activity choices for those periods. So, in general, we would expect that
qi(t)A would not equal qi(t)O and lj(t)A would not equal
lj(t)O for i = 1... Q, j= 1 ... L, and t = 0 ... T-1.
But our model implies different sets of human characteristics will develop under economic choice patterns
{ qi(t)A
, Ij(t)A}
and { qi(t)O, lj(t)O }
and,therefore, a different set of preference patterns for various comodity-work
bundles will develop as well.
This concludes the demonstration of Theorem
6.2 provided the proof does not rest on choice of the final period, T,
as the starting point. But the only convenience offered by this starting point
is that a particular change in relative prices can be translated into a shift
in the relative amounts of the two commodities consumed whose sign is determinant
under the assumption of diminishing marginal utilities. Had we begun with a
change of relative prices in any earlier time period, the direction of the shift
in the consumption bundle for that time period would not have been determinant
due to the many terms of indeterminate signs under the double summation signs.
However, it should be clear that, in general, changes would be required in the
values of any qm(t)
and qn(t),
for t = 0 ... (T-
1) to reestablish the necessary conditions after a change in the relative
prices pm(t)
and pn(t)
Once the ratio of prices in period t for any two commodities has
changed, no matter in what direction, changes will be required for all earlier
consumption and work activity choices with consequent changes in human characteristics
and preference structures exactly as argued above.
The phenomenon of rational adjustment of preferences, toward wanting what is
presumed will be most readily available and away from wanting what is presumed
will be difficult to obtain, should not be confused with another way that "utility"
might be a function of "price"--namely "snob effects," "keeping up with the
Joneses," or "conspicuous consumption. "
9 The clear difference between the phenomena can be appreciated by
noticing that the direction of the individual's adjustment is exactly opposite
in the two cases. Whereas the phenomenon we are discussing would lead rational
individuals to diminish their desires for goods whose future price was expected
to be high, the phenomenon of conspicuous consumption would lead individuals
to value goods with high prices more. We might point out there is no reason
both phenomena could not exist in the real world. But where it has been relatively
easy for neoclassical welfare theory to dismiss "snob effects" as irrational,
if not aberrant behavior, in which the individual at least "pays" for his snobbery,
the phenomenon we refer to is characterized precisely by its rationality and,
therefore, very much a "legitimate" focus of concern according to traditional
welfare criteria.